近日,信息科学与工程学院徐敬可副教授作为第一作者在《IEEE Transactions on Information Theory》在线发表了题为“Explicit Constructions of Capacity-Achieving T-PIR Schemes over Small Fields via Generalized Minor Matrices”的研究论文。该工作是徐敬可老师自2024年以来在该CCF-A期刊(IEEE TIT)上发表的又一重要进展。
私有信息检索(Private Information Retrieval, PIR),是信息安全领域的一个重要研究课题,主要关注的是如何在不泄露查询内容的前提下,从多个数据库中提取检索信息,如1图所示。PIR自从提出以来,已在军事、商业等领域有着重要应用。容量是衡量PIR方案效率的重要指标,而数据分包是设计达到容量的PIR方案的重要技术,如图2所示。然而现有的最优方案需要在很大的域上构造,这严重制约了方案的实用性。
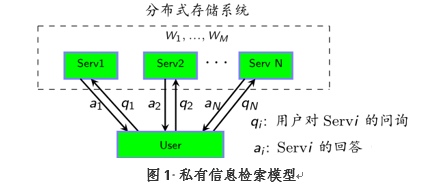
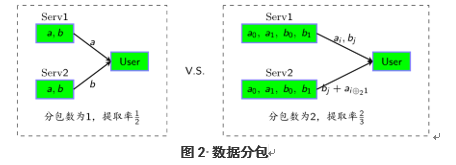
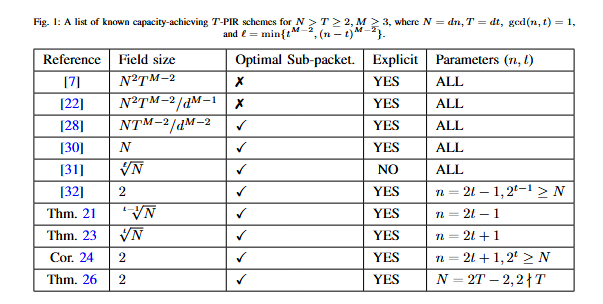
为了克服这一困难,本文创造性提出基于小域上MDS阵列码来构造的最优PIR方案。具体来说,首先利用M-1个具有特定类型信息集的MDS阵列码,设计了小域上分包最优且达到容量抗合谋保密信息提取方案的一般框架,从而最优PIR方案的构造问题转化为小域上具有特定信息集的MDS阵列码的构造问题。其次,利用乘积码与组合技巧将该问题转化为构造一个具有特定信息集的MDS阵列码。然后,应用加群陪集、Trace函数、幂和、线性化多项式的牛顿恒等式等理论基础发展出广义子式矩阵这一工具,进而刻画其各阶顺序主子式。最终,我们基于广义子式矩阵这一最新理论工具,成功构造出三大类小域上的最优PIR方案,具有结果与比较如表1所示。
本文的合作者还有山东大学方伟军教授。该研究得到了国家重点研发计划项目、国家自然科学基金项目、山东省自然科学基金项目、山东省泰山学者项目、山东省“青创团队计划”项目的资助。
原文链接:https://ieeexplore.ieee.org/document/10980207.
编 辑:万 千
审 核:贾 波








